HPVM Optimization Framework¶

The HPVM optimization framework comprises of DFG- and non-DFG- transformations as well as a Design Space Exploration (DSE) tool that uses these transformation. The transformations are described in this document.

HPVM transformations¶

Automatic Input Buffering¶

This transformation automatically finds read-only kernel (i.e., leaf node function) pointer arguments with constant size, and copies them from Global memory to Local memory buffers. The constant size is determined using a DFG traversal to determine the size of the argument as allocated in the host code. In DSE, one boolean parameter is created per pointer argument that determines whether or not the argument will get buffered. For example, if a given argument has locality and fits on the FPGA local memory, then DSE may select it for buffering in the final design if that improves performance.

Guided Argument Privatization¶

Privatizable arguments are ones that are completely generated and then read within the kernel. We require that they must be of fixed size. Such arguments may arise, e.g., when allocating all memory objects in main(). This transformation finds such arguments and creates private copies, converting all reads and writes to access Local instead of Global memory. Since finding privatizable variables is a difficult problem requiring interprocedural pointer analysis and array section analysis, we instead make this a guided optimization requiring the programmer to mark private arguments and their size in Hetero-C++, using a special keyword. This annotation is completely hardware-agnostic. In DSE, one boolean parameter is created per privatizable argument that determines if the arguments gets privatized. As such, only the ones that improve performance will be privatized in the final design.

Automatic `ivdep` Insertion¶

The ivdep pragma (with specified pointer parameters) informs AOC that a loop does not have loop-carried dependencies on the specified pointers. This may allow AOC to achieve lower initiation intervals when pipelining the loop. HPVM guarantees that dynamic node instances are parallel, i.e., there are no cross-instance dependencies due to pointer arguments. As such, we insert the pragma for any loop generated by Node Sequentialization, and pass in all pointer input parameters of the node as arguments to the array clause of ivdep. Since ivdep never hurts performance, it is always enabled in DSE.

Loop Unrolling¶

This transformation unrolls the loops of a leaf node function with known trip counts. For loops with variable trip counts, we added a Hetero-C++ marker function (isNonZeroLoop) which the programmer can use to specify the run-time trip count of each loop (obtained perhaps from profiling information). This marker function is not hardware specific, and its insertion can be automated in the future using an instrumentation pass. In DSE, an integer parameter is created for the unroll factor of each loop, including ones generated by Sequentialization. As such, DSE would unroll each loop the appropriate number of times to achieve the best performance.

Greedy Loop Fusion¶

This transformation fuses all the fusible loops of a leaf node function at each nesting level, going from the outermost nesting level to the innermost. At each level, we find the fusible loops by checking for matching loop bounds and no fusion-preventing dependencies. When ivdep is present, we also disallow a forward loop-carried dependence that is otherwise legal, since ivdep will no longer hold. Selectively removing these pointers from ivdep is part of future work. In DSE, one boolean parameter is created for every function with more than one loop, turning LF on or off for the entire function.

In general, LU and NF can extract pipeline parallelism together by unrolling outerloops and fusing innerloops. This is how the optimizer applies them when used without DSE.

Automatic Node Fusion¶

Node Fusion fuses multiple leaf nodes in the DFG into one node, merging their function bodies in what is effectively kernel fusion. Having the DFG representation makes it easy to identify nodes with source-sink relationships, allowing the compiler to focus on a subset of possible fusions that are likely to be profitable. In DSE, one boolean parameter is created for each pair of nodes that can legally be fused and are connected by an edge. As such, DSE tries to find the best combination of fused nodes that would maximize performance in the final design.

Automatic Task Parallelism¶

This optimization analyzes the DFG to determine if there exist any nodes that can run in parallel (i.e. have no connecting path in the DFG), and accordingly guides code generation to enable launching them in parallel on the FPGA. In DSE, one boolean parameter is created for the entire application, enabling task parallelism if it is profitable.

Node Tiling¶

This is an optimization that tiles the iteration space of a leaf node and its replication factor, analogous to loop tiling. It takes the node and nests it within a new internal node, giving it and the existing leaf node new replication factors so that the outer node iterates over a set of tiles, and the leaf node iterates within each tile. The two nodes correspond to the outer and inner loop nests that would be generated when tiling an ordinary loop in serial code. Tiling is parameterized by a vector of tile widths, one per dimension of the original node.

Design Space Exploration¶

Our optimization framework sets up the parameter space for DSE by performing a static analysis of the HPVM IR and extracting the corresponding parameters for every possible optimization. Then, it interacts with HyperMapper (HM) <https://github.com/luinardi/hypermapper>, where in every iteration HM sends a chosen design sample (i.e. set of values for the parameters) and waits for a response. For each sample, we apply the optimizations with the provided parameter values, and then estimate the execution time.

Our current framework provides an execution time estimation model for FPGA, described below. Alternatively, users have the option to provide their own estimation model using a script, as described here.

FPGA Execution Time model¶

To estimate execution time, we devised an analytical model that uses the loop Initiation Intervals (\(II\)), latencies of basic blocks (in cycles) (\(LAT\)), and kernels’ estimated frequency (\(Fmax\)), which we extract from AOC’s pre-synthesis report, in addition to the profiled loop trip counts (\(TC\)) provided using isNonZeroLoop. The total execution time is calculated as follows:

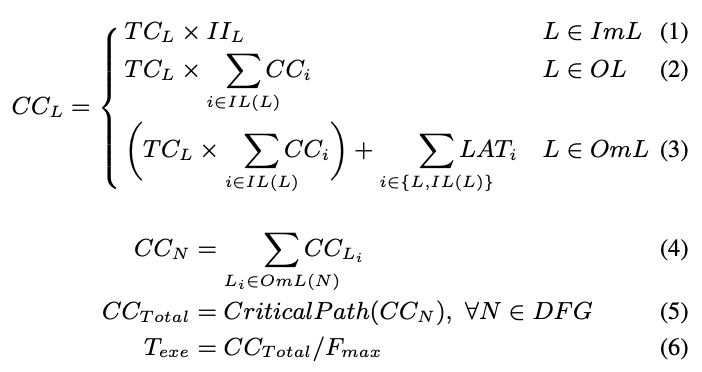
First, within a leaf node (kernel), the cycle count (\(CC_L\)) of a pipelined loop nest is calculated recursively such that: a) for every innermost loop it is the loop’s trip count times its initiation interval (Eq. 1); b) for every outer loop it is the loop’s trip count times the sum of all its inner loops’ cycle counts (Eq. 2); and c) for the outermost loop in the loop nest, it would be the same as (b) plus the total latency of all the basic blocks in all the loop nest bodies (i.e. time to drain the pipeline) (Eq. 3). If a loop nest is not pipelined, the \(LAT_i\) term should instead be added to every loop’s own cycle count. This is done in our estimation model, but omitted from the equations for simplicity.

Next, the cycle count of the DFG node (kernel) \(N\) is calculated as the sum of all the cycle counts of all the loop nests in that node (Eq. 4). The total cycle count of the accelerated portion of the application (i.e. the HPVM DFG) is calculated using a critical path analysis through the HPVM DFG (Eq. 5). Finally, the total execution time (in seconds) is calculated using Eq. 6.

We use the feasibility feature of HM which allows it to learn when a combination of parameter values may result in infeasible designs as DSE progresses. We determine the feasibility of a design point (i.e. whether or not it fits on the FPGA) by extracting the estimated resource utilization from the AOC reports. The estimated execution time and validity of the sample are then sent back to HM in our response.